Quaternion Graph Neural Networks

_{Dai Quoc Nguyen, 25 September, 2020}

1. Introduction
2. Quaternion Background
3. Quaternion Graph Neural Networks
4. Conclusion

Introduction

Recently, graph neural networks (GNNs) become a principal research direction to learn low-dimensional continuous embeddings for nodes and graphs. In general, GNNs use an Aggregation function [1, 2, 3] over neighbors of each node to update its vector representation iteratively. After that, GNNs utilize a ReadOut pooling function to obtain graph embeddings [4, 5, 6, 8].

Mathematically, given a graph G = (V, E, {h_v}_∀v∈V), where V is a set of nodes, E is a set of edges, and h_v is the Euclidean feature vector of node v ∈ V, we can formulate GNNs as follows:

h_v^(l+1) = Aggregation({h_u^(l)}_u∈Nv∪{v})

where h_v^(l) is the vector representation of node v at the l-th iteration/layer, N_v is the set of neighbors of node v, and h_v⁽⁰⁾ = h_v.

There have been many designs for the Aggregation functions proposed in recent literature [1, 7]. The widely-used one is introduced in Graph Convolutional Network (GCN) [1] as:

h_v^(l+1) = g(∑_u∈Nv∪{v} a_v,uW^(l) h_u^(l)), ∀ v ∈ V

where a_v,u is an edge constant between nodes v and u in the re-normalized adjacency matrix, W^(l) is a weight matrix, and g is a nonlinear activation function.

We can follow [7] to employ a concatenation over the vector representations of node v across the different layers to construct the node embedding e_v. The graph-level ReadOut function can be a simple sum pooling or a complex pooling such as sort pooling [5], hierarchical pooling [8], and differentiable pooling [6]. As the sum pooling produces competitive accuracies for graph classification task [7], we can utilize the sum pooling to obtain the embedding e_G of the entire graph G as: e_G = ∑_∀v∈V e_v.

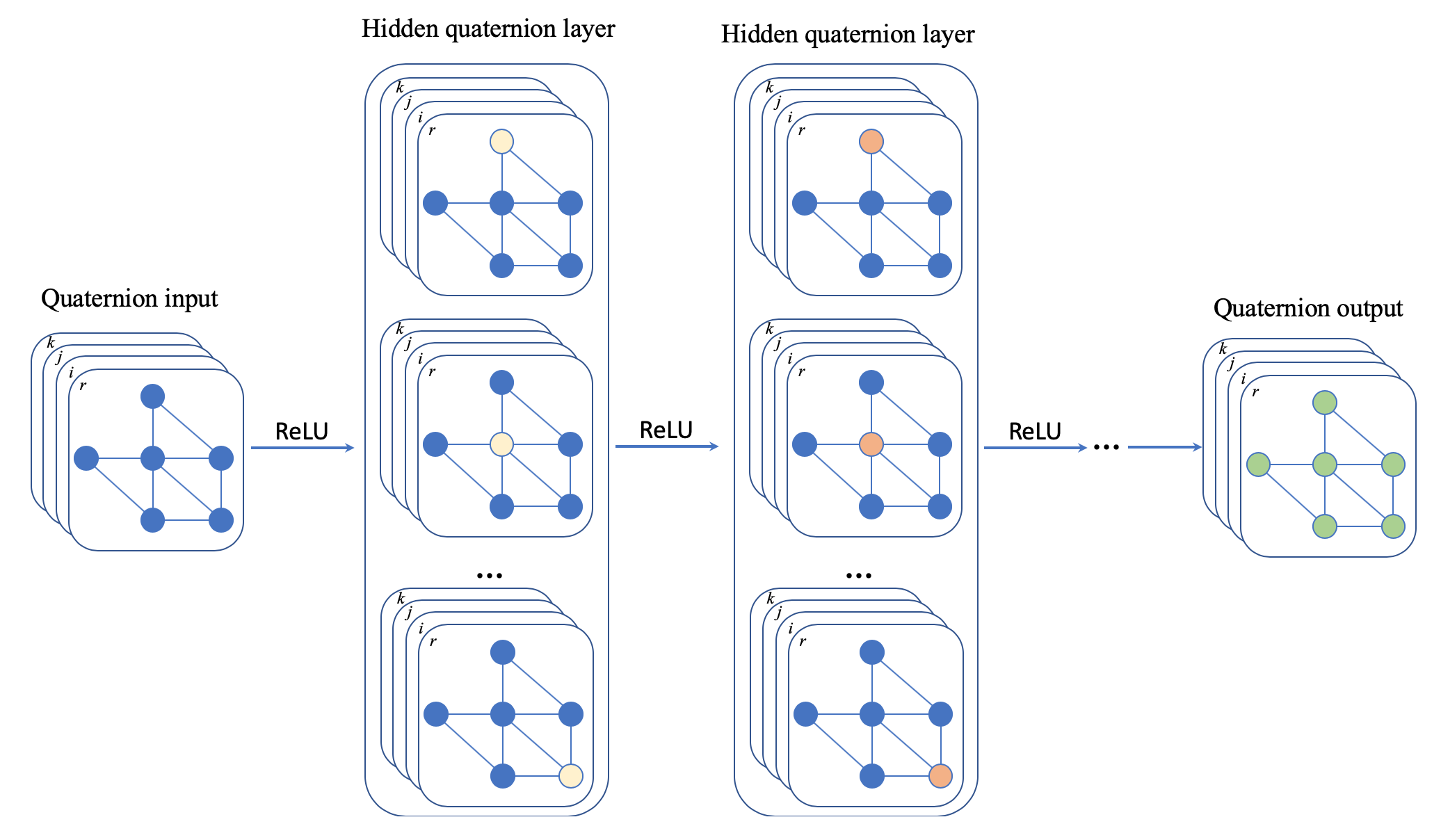
While it has been considered under other contexts, in this blog, we address the following question: Can we move beyond the Euclidean space to learn better graph representations? To this end, we propose to learn embeddings for nodes and graphs within the Quaternion space and introduce a novel form of Quaternion Graph Neural Networks (QGNN).

Quaternion Background

The Quaternion space has been applied to image classification [10, 11], speech recognition [12, 13], knowledge graph completion [14], and machine translation [15]. A quaternion q ∈ H is a hyper-complex number [9], consisting of a real and three separate imaginary components, which is defined as:

q = q_r + q_ii + q_jj + q_kk

where q_r, q_i, q_j, q_k ∈ R, and i, j, k are imaginary units that ijk = i² = j² = k² = −1, leads to non-commutative multiplication rules as ij = k, ji = −k, jk = i, kj = −i, ki = j, and ik = −j. Correspondingly, a n-dimensional quaternion vector q ∈ Hⁿ is defined as:

q = q_r + q_ii + q_jj + q_kk

where q_r, q_i, q_j, q_k ∈ Rⁿ. The operations for the Quaternion algebra are defined as follows:

• Conjugate. The conjugate q^* of a quaternion q is defined as: q^* = q_r - q_ii - q_jj - q_kk

• Addition. The addition of two quaternions q and p is defined as: q + p = (q_r + p_r) + (q_i + p_i)i + (q_j + p_j)j + (q_k + p_k)k

• Scalar multiplication. The multiplication of a scalar λ and a quaternion q is defined as: λq = λq_r + λq_ii + λq_jj + λq_kk

• Norm. The norm ‖q‖ of a quaternion q is defined as: ‖q‖ = sqrt(q_r² + q_i² + q_j² + q_k²)

• Hamilton product. The Hamilton product ⊗ (i.e., the quaternion multiplication) of two quaternions q and p is defined as:

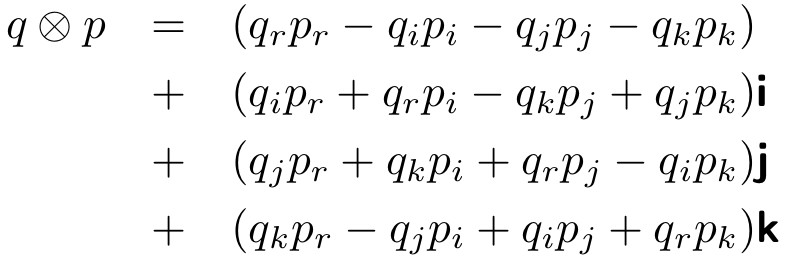
• Note that the Hamilton product is not commutative, i.e., q ⊗ p ≠ p ⊗ q.

• Concatenation. A concatenation of two quaternion vectors q and p is defined as: [q; p] = [q_r; p_r] + [q_i; p_i]i + [q_j; p_j]j + [q_k; p_k]k

Quaternion Graph Neural Networks

In our QGNN, the Aggregation function at the l-th layer is defined as:

h_v^(l+1),Q = g(∑_u∈Nv∪{v} a_v,uW^(l),Q ⊗ h_u^(l),Q), ∀ v ∈ V

where we use the superscript ^Q to denote the Quaternion space; a_v,u is an edge constant between nodes v and u in the re-normalized adjacency matrix; W^(l),Q is a quaternion weight matrix; h_u^(0),Q is the quaternion feature vector of node v; and g can be a nonlinear activation function such as ReLU, and g is adopted to each quaternion element [12] as: g(q) = g(q_r) + g(q_i)i + g(q_j)j + g(q_k)k.

We also represent the quaternion vector h_u^(l),Q ∈ Hⁿ and the quaternion weight matrix W^(l),Q ∈ H^mxn as:

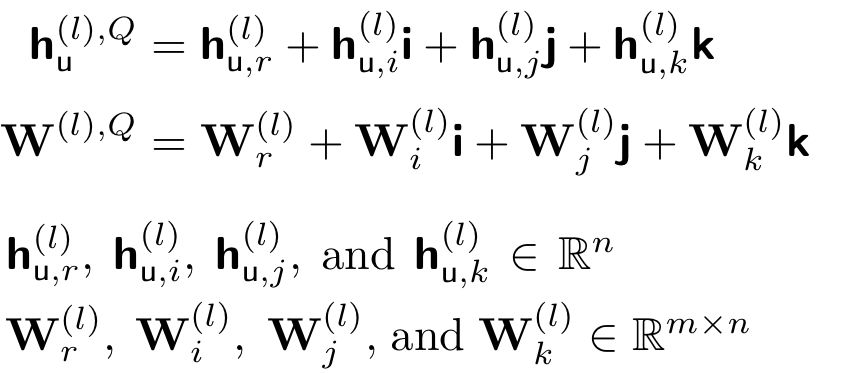
We now express the Hamilton product ⊗ between W^(l),Q and h_u^(l),Q as:

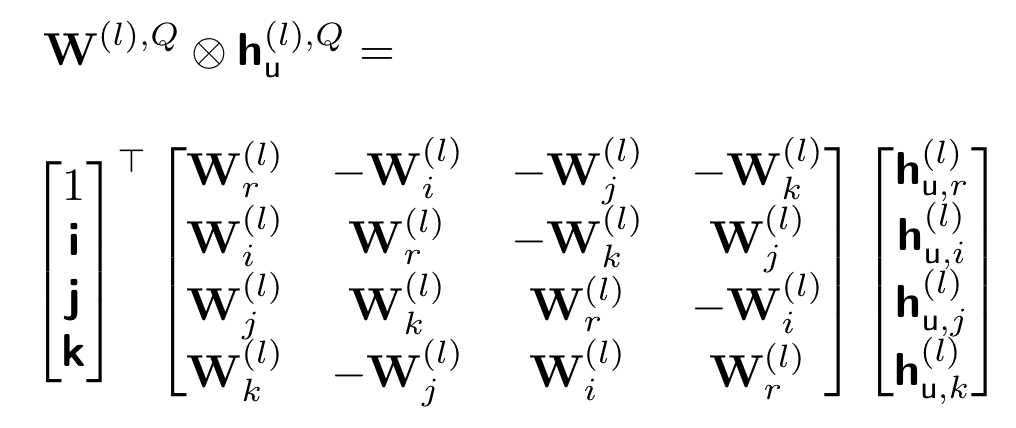
If we use any slight change in the input h_u^(l),Q, we get an entirely different output [16], leading to a different performance. This phenomenon is one of the crucial reasons why the Quaternion space provides highly expressive computations through the Hamilton product compared to the Euclidean and complex vector spaces. The phenomenon enforces the model to learn the potential relations within each hidden layer and between the different hidden layers, hence increasing the graph representation quality.

QGNN for semi-supervised node classification. We consider h_v^(L),Q, which is the quaternion vector representation of node v at the last L-th QGNN layer. To predict the label of node v, we simply feed h_v^(L),Q to a prediction layer followed by a softmax layer as follows:

ŷ_v = softmax(∑_u∈Nv∪{v} a_v,uW Vec(h_v^(L),Q)), ∀ v ∈ V

where Vec(.) denotes a concatenation of the four components of the quaternion vector. For example,

Vec(h_v^(L),Q) = [h_v,r^(L); h_v,i^(L); h_v,j^(L); h_v,k^(L)]

QGNN for graph classification. We employ a concatenation over the vector representations h_v^(l),Q of node v at the different QGNN layers to construct the node embedding e_v^Q. And then we use the sum pooling to obtain the embedding e_G^Q of the entire graph G as: e_G^Q = ∑_∀v∈V e_v^Q. To perform the graph classification task, we also use Vec(.) to vectorize e_G^Q, which is then fed to a single fully-connected layer followed by the softmax layer to predict the graph label.

Conclusion

As this work represents a fundamental research problem in representing graphs, QGNN has demonstrated to be useful through experimental evaluations for downstream tasks such as graph classification and node classification.

Please cite our paper whenever QGNN is used to produce published results or incorporated into other software:

@article{Nguyen2020QGNN,
	author={Dai Quoc Nguyen and Tu Dinh Nguyen and Dinh Phung},
	title={Quaternion Graph Neural Networks},
	journal={arXiv preprint arXiv:2008.05089},
	year={2020}
}

References

[1] Thomas N. Kipf and Max Welling. Semi-supervised classification with graph convolutional networks. In Proceedings of the International Conference on Learning Representations (ICLR), 2017.

[2] William L. Hamilton, Rex Ying, and Jure Leskovec. Inductive representation learning on large graphs. In Proceedings of the Advances in Neural Information Processing Systems, pages 1024–1034, 2017.

[3] Petar Veličković, Guillem Cucurull, Arantxa Casanova, Adriana Romero, Pietro Liò, and Yoshua Bengio. Graph Attention Networks. In Proceedings of the International Conference on Learning Representations(ICLR), 2018.

[4] Justin Gilmer, Samuel S. Schoenholz, Patrick F. Riley, Oriol Vinyals, and George E. Dahl. Neural Message Passing for Quantum Chemistry. In Proceedings of the International Conference on Machine Learning, pages 1263–1272, 2017.

[5] Muhan Zhang, Zhicheng Cui, Marion Neumann, and Yixin Chen. An End-to-End Deep Learning Architecture for Graph Classification. In Proceedings of the AAAI Conference on Artificial Intelligence, 2018.

[6] Rex Ying, Jiaxuan You, Christopher Morris, Xiang Ren, William L. Hamilton, and Jure Leskovec. Hierarchical graph representation learning with differentiable pooling. In Proceedings of the Advances in Neural Information Processing Systems, pages 4805–4815, 2018.

[7] Keyulu Xu, Weihua Hu, Jure Leskovec, and Stefanie Jegelka. How Powerful Are Graph Neural Networks? In Proceedings of the International Conference on Learning Representations (ICLR), 2019.

[8] Cătălina Cangea, Petar Veličković, Nikola Jovanović, Thomas Kipf, and Pietro Liò. Towards sparse hierarchical graph classifiers. arXiv preprint arXiv:1811.01287, 2018.

[9] William Rowan Hamilton. Ii. on quaternions; or on a new system of imaginaries in algebra. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 25(163):10–13,1844.

[10] Xuanyu Zhu, Yi Xu, Hongteng Xu, and Changjian Chen. Quaternion convolutional neural networks. In Proceedings of the European Conference on Computer Vision (ECCV), pages631–647, 2018.

[11] Chase J Gaudet and Anthony S Maida. Deep quaternion networks. In Proceedings of the International Joint Conference on Neural Networks (IJCNN), pages 1–8, 2018.

[12] Titouan Parcollet, Mirco Ravanelli, Mohamed Morchid, Georges Linarès, Chiheb Trabelsi,Renato De Mori, and Yoshua Bengio. Quaternion recurrent neural networks. In Proceedings of the International Conference on Learning Representations (ICLR), 2019.

[13] Titouan Parcollet, Ying Zhang, Mohamed Morchid, Chiheb Trabelsi, Georges Linarès, RenatoDe Mori, and Yoshua Bengio. Quaternion convolutional neural networks for end-to-end automatic speech recognition. In Proceedings of the Interspeech, pages 22–26, 2018.

[14] Shuai Zhang, Yi Tay, Lina Yao, and Qi Liu. Quaternion knowledge graph embeddings. In Proceedings of the Advances in Neural Information Processing Systems, pages 2731–2741, 2019.

[15] Yi Tay, Aston Zhang, Anh Tuan Luu, Jinfeng Rao, Shuai Zhang, Shuohang Wang, Jie Fu, and Siu Cheung Hui. Lightweight and efficient neural natural language processing with quaternion networks. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, pages 1494–1503, 2019.

[16] Titouan Parcollet, Mohamed Morchid, and Georges Linarès. A survey of quaternion neural networks. Artificial Intelligence Review, pages 1–26, 2019.